توجه: مقاله زیر در وبلاگ جف اتوود به صورت یک سه گانه منتشر شده است که در اینجا به صورت پیوسته مشاهده میکنید.
فصل دوم از کتاب «تخمین نرمافزار: رفع ابهام از هنر سیاه» (Software estimation: Demystifying the black art) با یک آزمون آغاز میشود که برای سنجش تواناییهای شما در تخمین طراحی شده است. این تمرین جالبی است و فکر کردم شاید همه بخواهند آن را امتحان کنند.
- برای هر سؤال، محدودههای حداقل و حداکثر را طوری مشخص کنید که ۹۰ درصد احتمال داشته باشید مقدار درست را شامل شود.
- محدودههای خود را خیلی باریک یا بیش از حد گسترده نکنید، اما مطمئن شوید که به اندازهای وسیع است که ۹۰ درصد احتمال میدهد مقدار درست را شامل شود.
- پاسخها را از اینترنت جستجو نکنید.
- شما باید برای هر سؤال محدودهای به عنوان تخمین ارائه دهید.
- برای این آزمون بیشتر از ۱۰ دقیقه وقت نگذارید.
خب، چقدر در تخمین زدن مهارت دارید؟
| سوال | کمترین تخمین | بیشترین تخمین |
| دمای سطح خورشید | ||
| عرض جغرافیایی شانگهای (Shanghai) | ||
| مساحت قاره آسیا | ||
| سال تولد اسکندر بزرگ (Alexander the Great) | ||
| مجموع ارزش ارزهای در گردش آمریکا در سال ۲۰۰۴ | ||
| حجم کل دریاچههای بزرگ | ||
| میزان فروش جهانی فیلم تایتانیک (Titanic) | ||
| طول کل خط ساحلی اقیانوس آرام | ||
| تعداد عناوین کتابهای منتشر شده در آمریکا از سال ۱۷۷۶ | ||
| بزرگترین نهنگ آبی که تاکنون ثبت شده است |
به یاد داشته باشید، هدف این آزمون تعیین این نیست که آیا شما «کن جنینگز» (Ken Jennings) بعدی هستید یا نه. این درباره تخمین است، نه اطلاعات عمومی.
اگر نگرانید که چنین آزمونی هیچ ارتباطی با توسعه نرمافزار ندارد، به این نکات توجه کنید:
در حوزه نرمافزار، از شما به ندرت خواسته میشود حجم دریاچههای بزرگ یا دمای سطح خورشید را تخمین بزنید. آیا منطقی است از شما انتظار داشته باشند بتوانید مقدار ارزهای در گردش در آمریکا یا تعداد کتابهای منتشر شده در این کشور را تخمین بزنید، بهویژه اگر در آمریکا نباشید؟
توسعهدهندگان نرمافزار اغلب موظف به تخمین پروژهها در حوزههای تجاری ناآشنا، پروژههایی که با فناوریهای جدید پیادهسازی میشوند، تأثیر ابزارهای جدید برنامهنویسی بر بهرهوری، بهرهوری افرادی که هنوز شناسایی نشدهاند و مواردی از این دست هستند. تخمین زدن در شرایط عدم قطعیت برای تخمینزنندگان نرمافزار یک امر عادی است.
بقیه مطالب کتاب [«تخمین نرمافزار: رفع ابهام از هنر سیاه»] توضیح میدهد که چگونه در چنین شرایطی موفق شوید.
| سوال | جواب |
| دمای سطح خورشید | ۶۰۰۰ درجه سانتیگراد |
| عرض جغرافیایی شانگهای (Shanghai) | ۳۱ شمالی |
| مساحت قاره آسیا | ۴۴۳۹۰۰۰۰ کیلومتر مربع |
| سال تولد اسکندر بزرگ (Alexander the Great) | ۳۵۶ قبل از میلاد |
| مجموع ارزش ارزهای در گردش آمریکا در سال ۲۰۰۴ | ۷۱۹.۹ میلیارد دلار |
| حجم کل دریاچههای بزرگ | ۲۳۰۰۰ کیلومتر مربع |
| میزان فروش جهانی فیلم تایتانیک (Titanic) | ۱.۸۳۵ میلیارد دلار |
| طول کل خط ساحلی اقیانوس آرام | ۱۳۵۶۶۳ کیلومتر |
| تعداد عناوین کتابهای منتشر شده در آمریکا از سال ۱۷۷۶ | ۲۲ میلیون |
| بزرگترین نهنگ آبی که تاکنون ثبت شده است | ۱۷۰ تن |
هدف خاص این تمرین این بود که با سطح اطمینان ۹۰ درصد تخمین بزنید. در این آزمون ۱۰ سؤال وجود دارد، بنابراین اگر واقعاً با سطح اطمینان ۹۰ درصد تخمین زده باشید، باید تقریباً ۹ پاسخ صحیح داشته باشید. «مککانل» (McConnell) این آزمون را به هر شرکتکننده در دوره تخمین خود میدهد. نتایج در نمودار زیر نمایش داده شده است.
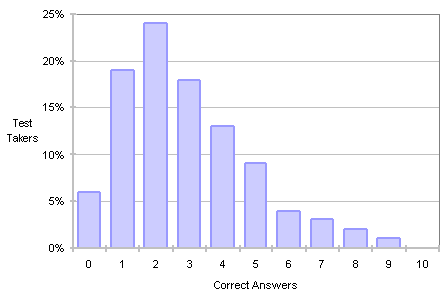
او این تحلیل را از دادهها ارائه میدهد:
برای افرادی که نتایجشان در تصویر نشان داده شده است، میانگین تعداد پاسخهای صحیح ۲.۸ است. تنها ۲ درصد از شرکتکنندگان در آزمون ۸ پاسخ یا بیشتر را درست پاسخ میدهند. هیچکس تاکنون موفق به پاسخ دادن صحیح به هر ۱۰ سؤال نشده است. به این نتیجه رسیدهام که حس شهودی اکثر مردم از «۹۰ درصد اطمینان» در واقع بیشتر شبیه به «۳۰ درصد اطمینان» است. مطالعات دیگر نیز این یافته اساسی را تأیید کردهاند (Zultner 1999, Jrgensen 2002).
به علاوه، تعداد کمی از افرادی که موفق به نزدیک شدن به هدف ~۹ پاسخ صحیح میشوند، معمولاً احساس میکنند اشتباهی مرتکب شدهاند:
وقتی فردی نادر را پیدا میکنم که ۷ یا ۸ پاسخ صحیح داشته باشد، از او میپرسم: «چطور این تعداد پاسخ صحیح داشتید؟» پاسخ معمول چیست؟ «محدودههایم را بیش از حد وسیع در نظر گرفتم.»
پاسخ من این است: «نه، اینطور نیست! شما محدودههای خود را به اندازه کافی وسیع نکردهاید!» اگر فقط ۷ یا ۸ پاسخ صحیح دارید، محدودههایتان هنوز هم به اندازه کافی وسیع نبوده تا پاسخ درست را به همان اندازهای که باید شامل شود.
ما عادت کردهایم باور کنیم که تخمینهایی با محدودههای باریک دقیقتر از تخمینهایی با محدودههای وسیع هستند. ما بر این باوریم که محدودههای وسیع باعث میشوند بیاطلاع یا ناتوان به نظر برسیم. اما معمولاً عکس این موضوع درست است.
خب، از این تمرین چه آموختیم؟
- وقتی از کسی میخواهید محدودهای ارائه دهد که ۹۰ درصد اطمینان فراهم کند، انتظار داشته باشید به طور میانگین ۳۰ درصد اطمینان داشته باشد.
- مردم ذاتاً از ارائه محدودههای وسیع پرهیز میکنند – حتی زمانی که سطح اطمینان به یک محدوده وسیع نیاز دارد تا دقیق باشد – زیرا احساس میکنند تخمینهای باریک نشانه یک تخمین بهتر است.
تخمینهای باریک خود ویرانگر هستند، اما متأسفانه این طبیعت انسانی است. مگر اینکه دادههای مشخصی داشته باشید که از تخمین باریک شما پشتیبانی کند، احتمالاً تخمین شما باید وسیعتر از چیزی باشد که در نظر گرفتهاید.
فرض کنید در یک مهمانی برای بهترین تخمینزنندگان نرمافزار در دنیا حضور دارید. اتاق پر از جمعیت است و شما در وسط اتاق، کنار سه تخمینزننده دیگر نشستهاید. وقتی اتاق را از نظر میگذرانید، فقط تخمینزنندگان را میبینید که دیوار به دیوار نشستهاند. ناگهان، مجری به سمت میکروفن میرود و میگوید: «باید دقیقاً بدانیم چند نفر در اتاق حضور دارند تا بتوانیم برای دسر سفارش دهیم. چه کسی میتواند دقیقترین تخمین را برای تعداد افراد حاضر در اتاق ارائه دهد؟»
بیل (Bill)، تخمینزننده سمت راست شما، میگوید: «من در تخمین زدن جمعیت مهارت دارم. با توجه به تجربهام، به نظر میرسد حدود ۳۳۵ نفر در اتاق هستند.»
تخمینزننده روبهروی شما، کارل (Karl)، میگوید: «این اتاق دارای ۱۱ میز در عرض و ۷ میز در عمق است. یکی از دوستان من برگزارکننده مراسم است و به من گفته که برای هر میز ۵ نفر در نظر گرفته میشود. به نظر میرسد اکثر میزها واقعاً حدود ۵ نفر دارند. اگر ۱۱ را در ۷ و سپس در ۵ ضرب کنیم، به ۳۸۵ نفر میرسیم. فکر میکنم باید از این بهعنوان تخمین خود استفاده کنیم.»
تخمینزننده سمت چپ شما، لوسی (Lucy)، میگوید: «من هنگام ورود به اتاق متوجه شدم که تابلو ظرفیت اتاق نشان میدهد اینجا میتواند ۴۸۵ نفر را جا دهد. این اتاق تقریباً پر است. من فکر میکنم ۷۰ تا ۸۰ درصد پر است. اگر این درصدها را در ظرفیت اتاق ضرب کنیم، به ۳۴۰ تا ۳۸۸ نفر میرسیم. بیایید میانگین ۳۶۴ نفر را استفاده کنیم، یا شاید سادهتر باشد اگر بگوییم ۳۶۵ نفر.»
بیل میگوید: «ما تخمینهایی به ترتیب ۳۳۵، ۳۶۵ و ۳۸۵ نفر داریم. به نظر میرسد پاسخ صحیح در این میان باشد. من با ۳۶۵ راحت هستم.»
همه به شما نگاه میکنند. شما میگویید: «باید چیزی را بررسی کنم. آیا اجازه میدهید یک لحظه بیرون بروم؟»
چند دقیقه بعد بازمیگردید. «یادتان هست که باید بلیتهای خود را قبل از ورود به اتاق اسکن میکردیم؟ هنگام ورود به اتاق متوجه شدم که دستگاه دستی اسکن بلیتها یک شمارنده دارد. بنابراین برگشتم و با مسئول بلیت درب ورودی صحبت کردم. او گفت که طبق شمارش دستگاه، ۴۰۷ بلیت اسکن کرده است. همچنین گفت که تا این لحظه کسی اتاق را ترک نکرده است. فکر میکنم باید ۴۰۷ را بهعنوان تخمین خود در نظر بگیریم. نظر شما چیست؟»
نتیجهگیری این داستان واضح است: شما باید از تخمین زدن چیزی که میتوانید بشمارید، پرهیز کنید. و اگر امکان شمارش ندارید، حداقل باید سعی کنید تخمین خود را بر اساس یک عدد مرتبط محاسبه کنید، همانطور که کارل در این مثال انجام داد. بدترین نوع تخمین، تخمینهایی است که فقط بر اساس قضاوت انجام شدهاند – تخمینهایی که از هیچ نوع عدد واقعی استخراج نشدهاند.
هنر واقعی در تخمین نرمافزار، در واقع جستجوی سریع برای نقاط دادهای است که بتوانید تخمینهای خود را بر اساس آنها انجام دهید. خوشبختانه، اگر در سازمانی کار میکنید که دادههای تاریخی پروژهها را ثبت میکند، خوششانس هستید.
چه نوع مواردی را میتوانید در یک پروژه نرمافزاری بشمارید؟ در واقع موارد زیادی:
- نیازمندیهای بازاریابی
- ویژگیها
- موارد استفاده (Use cases)
- داستانها (Stories)
- نیازمندیهای فنی
- نقاط عملکرد
- درخواستهای تغییر
- صفحات وب
- گزارشها
- جعبههای گفتوگو
- جداول پایگاه داده (یا رویهها، نماها و غیره)
- کلاسها
- اشکالات یافتشده
- تنظیمات پیکربندی
- خطوط کد
- موارد آزمون (Test cases)
- تغییرات کد (Code churn)
هنر ساخت تخمین از نقاط مرجع شناختهشده موضوع جدیدی در علم کامپیوتر نیست. یکی از فصلهای موردعلاقه من در کتاب «Programming Pearls» درباره این است که چقدر محاسبات تقریباً ذهنی برای توسعه نرمافزار ضروری هستند:
«در میان یک گفتگوی جذاب در مهندسی نرمافزار بودم که باب مارتین (Bob Martin) از من پرسید: «چقدر آب در روز از رودخانه میسیسیپی جاری میشود؟» چون دیدگاههای او تا آن لحظه برایم بسیار جالب بود، بهطور مؤدبانه پاسخ واقعیام را فروخوردم و گفتم: «ببخشید؟» وقتی او دوباره پرسید، فهمیدم که چارهای ندارم جز اینکه همراهیاش کنم؛ مرد بیچاره که آشکارا زیر فشارهای اداره یک شرکت بزرگ نرمافزاری قرار گرفته بود.
پاسخم چیزی شبیه به این بود: من تخمین زدم که نزدیکی دهانه رودخانه حدود یک مایل عرض و شاید بیست فوت عمق دارد (یا حدود یک دویست و پنجاهم یک مایل). فرض کردم که نرخ جریان پنج مایل در ساعت است، یا صد و بیست مایل در روز. ضرب کردن:
۱ مایل x ۱/۲۵۰ مایل x ۱۲۰ مایل/روز ~ ۱/۲ مایل³/روز
نشان میداد که رودخانه حدود نصف مایل مکعب آب در روز تخلیه میکند، تا حدود یک مرتبه بزرگی. اما خب، که چه؟»
در آن لحظه، مارتین از روی میز خود پیشنهادی برای سیستم ارتباطی که سازمانش برای بازیهای المپیک تابستانی میساخت را برداشت و محاسبات مشابهی انجام داد. او در حین صحبت یک پارامتر کلیدی را با اندازهگیری زمان ارسال یک کاراکتر ایمیل به خودش تخمین زد. بقیه اعدادش مستقیماً از پیشنهاد گرفته شده و به همین دلیل بسیار دقیق بودند. محاسباتش به سادگی همان محاسبات مربوط به رودخانه میسیسیپی و بسیار روشنگرتر بود. آنها نشان دادند که، تحت مفروضات سخاوتمندانه، سیستم پیشنهادی فقط در صورتی میتواند کار کند که حداقل ۱۲۰ ثانیه در هر دقیقه وجود داشته باشد. او روز قبل طراحی را به مرحله بازنگری بازگردانده بود. (این گفتگو حدود یک سال قبل از رویداد انجام شد و سیستم نهایی در طول بازیهای المپیک بدون هیچ مشکلی استفاده شد.)
این روش عالی (اگرچه عجیب) باب مارتین برای معرفی تکنیک مهندسی «محاسبات تقریبی ذهنی» بود. این ایده در مدارس مهندسی استاندارد است و برای اکثر مهندسان عملی به نان و کره میماند. متأسفانه، این روش در دنیای کامپیوتر اغلب نادیده گرفته میشود.»
استیو بوش (Steve Bush) در یکی از دیدگاههای اخیر اشاره کرد که فیزیکدان انریکو فِرمی (Enrico Fermi) به این نوع محاسبات مشهور بود و ظاهراً عبارت «محاسبه تقریب ذهنی» را او ابداع کرده است.
این محاسبات معمولاً به شکل «سؤالات فرمی» ارائه میشوند؛ سؤال مرسوم فرمی این است که چند تنظیمکننده پیانو در شیکاگو وجود دارد؟
- طبق سالنامه، میدانیم که شیکاگو جمعیتی حدود ۳ میلیون نفر دارد.
- فرض کنید میانگین تعداد افراد در هر خانواده چهار نفر باشد. تعداد خانوادههای شیکاگو حدود ۷۵۰ هزار است.
- اگر از هر پنج خانواده یکی دارای پیانو باشد، ۱۵۰ هزار پیانو در شیکاگو وجود خواهد داشت.
- اگر یک تنظیمکننده پیانو به طور متوسط هر روز چهار پیانو را تنظیم کند و پنج روز در هفته کار کند، در یک سال (۵۲ هفته) ۱۰۰۰ پیانو را تنظیم خواهد کرد.
- ۱۵ هزار / (۴ x ۵ x ۵۰) = ۱۵۰
- حدوداً ۱۵۰ تنظیمکننده پیانو در شیکاگو وجود دارد.
سؤالات فِرمی جالب هستند، زیرا پاسخ واقعی سؤال در مقایسه با فرآیندی که برای رسیدن به آن طی میکنید اهمیت ثانویه دارد. آیا حدس زدید؟ یا تخمین زدید؟


